The Modified Internal Rate of Return, often just called the MIRR, is a powerful and frequently used investment performance indicator. Yet, it’s commonly misunderstood by many finance and commercial real estate professionals. In this post, we’ll take a deep dive into the concept of the MIRR. We’ll define the MIRR, look at the logic and intuition behind the MIRR, dispel some common mistakes and misconceptions, and finally, we’ll tie it all together with a relevant example.
What is MIRR?
First, what is the definition of MIRR? The Modified Internal Rate of Return (MIRR) is a variation of the traditional Internal Rate of Return (IRR) calculation in that it computes IRR with explicit reinvestment rate and finance rate assumptions. The MIRR accounts for the reinvestment of any positive interim cash flows by using a reinvestment rate, and it also accounts for any negative cash flows by using a finance rate (also known as a safe rate).
The reason why these two rates are used is that it allows for any positive cash flows thrown off by an investment over the holding period to be reinvested at the “reinvestment rate”. It also allows any negative cash flows to be discounted back to the present time at the “finance rate” to determine how much needs to be set aside today to fund the future cash outflows.
By using this approach, the MIRR boils a set of cash flows down to just two numbers: 1) a single initial investment amount at the present time and 2) a total accumulated capital amount at the end of the holding period. Then, a single rate of return can be calculated using only these two numbers, which results in what’s known as the MIRR.
MIRR Example
Let’s take an example of the modified internal rate of return to see how this works. Suppose we have the following set of cash flows:
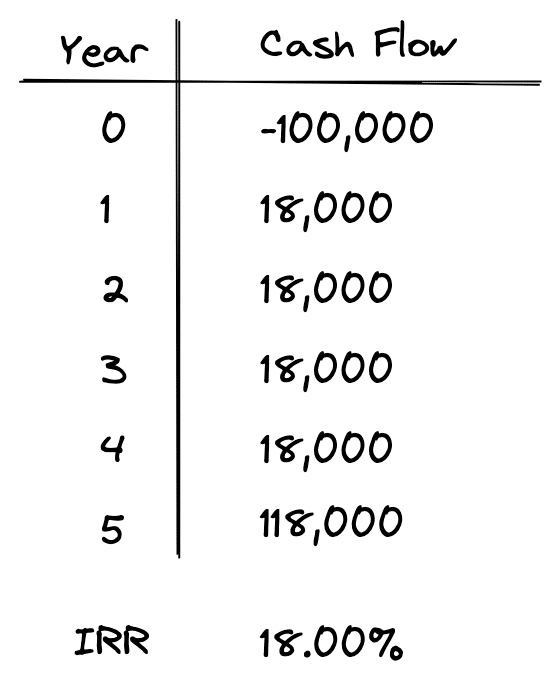
We invest $100,000 today and in return, we receive $18,000 per year for 5 years, plus at the end of year 5 we sell the asset and get back $100,000. If we use the traditional Internal Rate of Return (IRR) calculation, we get an IRR of 18%.
As you may recall, one of the problems with the traditional IRR calculation is that it doesn’t account for the reinvestment of interim cash flows. So, how can we use the Modified Internal Rate of Return to eliminate this problem?
First, let’s explicitly define a reinvestment rate for all the $18,000 interim cash flows. To account for the yield we can earn on these interim cash flows, let’s assume we can reinvest them at 10%. Note that this rate is lower than the above calculated IRR. This could be for a variety of reasons. For example, perhaps we can’t find any other investments that yield higher than 10%.
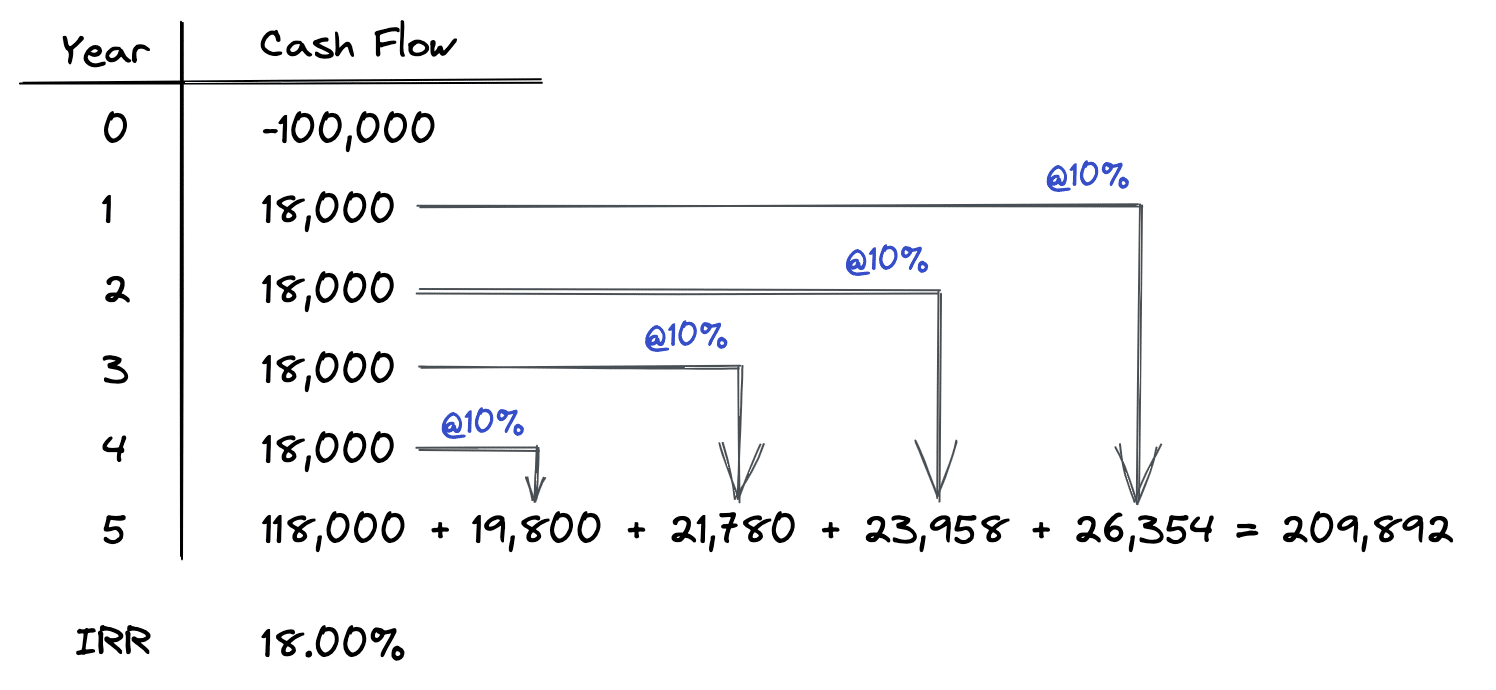
As shown above, we simply take each of our interim cash flows of $18,000 and then compound them forward at a rate of 10% to the end of year 5. When we add up all of our cash flows at the end of year 5 we get a total of $209,892. By doing this, we have transformed our initial set of cash flows into a different time value of money problem, which considers the yield we earn on interim cash flows that are reinvested elsewhere. Now we can simply take our new set of cash flows and solve for the IRR, which in this case is actually the MIRR since it’s based on our modified set of cash flows.
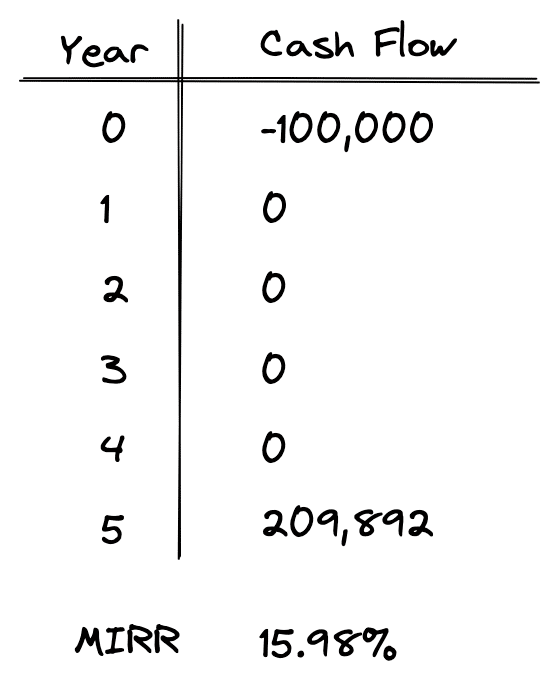
As you can see, the MIRR when using a 10% reinvestment rate is 15.98%. This is less than the 18% IRR we initially calculated above. Intuitively, it’s lower than our original IRR because we are reinvesting the interim cash flows at a rate lower than 18%. Also take note again that the MIRR calculation here is simply the IRR calculation. The only difference is that now we’ve transformed our initial set of cash flows into a new, modified, set of cash flows. That means that when we now calculate the IRR, it’s a modified IRR.
MIRR Example With Negative Cash Flows
Using the reinvestment rate on positive interim cash flows like we did above is how MIRR is commonly used, but sometimes there is more than one negative cash outflow during the holding period. Consider the following set of cash flows:
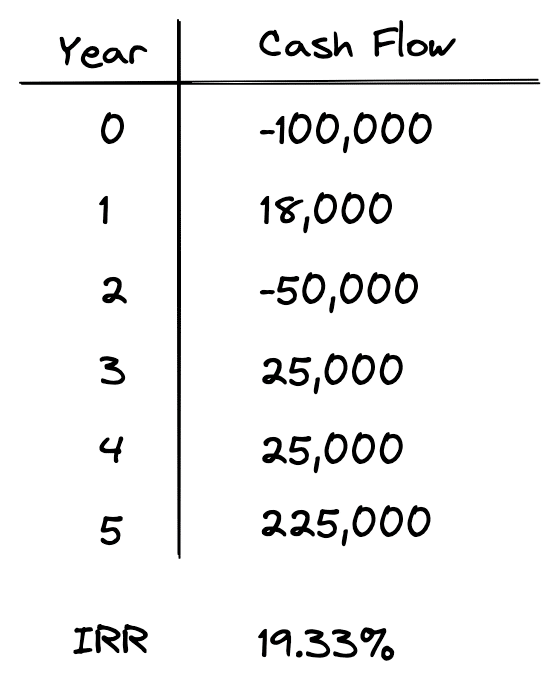
We have the same initial $100,000 upfront investment, but now we also have to come out of pocket $50,000 in year 2 for a capital expenditure. However, once this improvement is realized, our cash flows increases from $18,000 to $25,000, and now we can also sell the property at the end of year 5 for a higher price. This results in a higher IRR of 19.33%, but what does it do to our MIRR?
Let’s first tackle the positive interim cash flows by compounding them forward to the end of year 5.
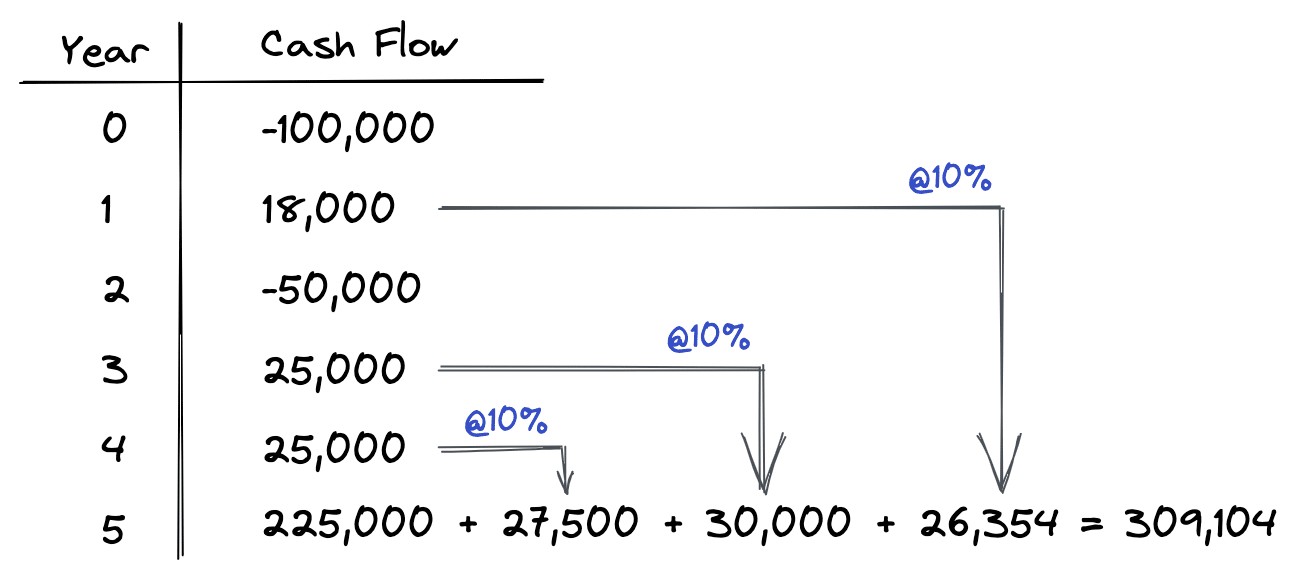
This is the same process we followed in our first MIRR example, but now we simply ignore the negative cash outflow in year 2. This leaves us with a -$100,000 initial investment, a -$50,000 cash outflow in year 2, and a $309,104 cash inflow at the end of year 5. Next, let’s discount our -$50,000 outflow back to the present time at our finance rate or safe rate.
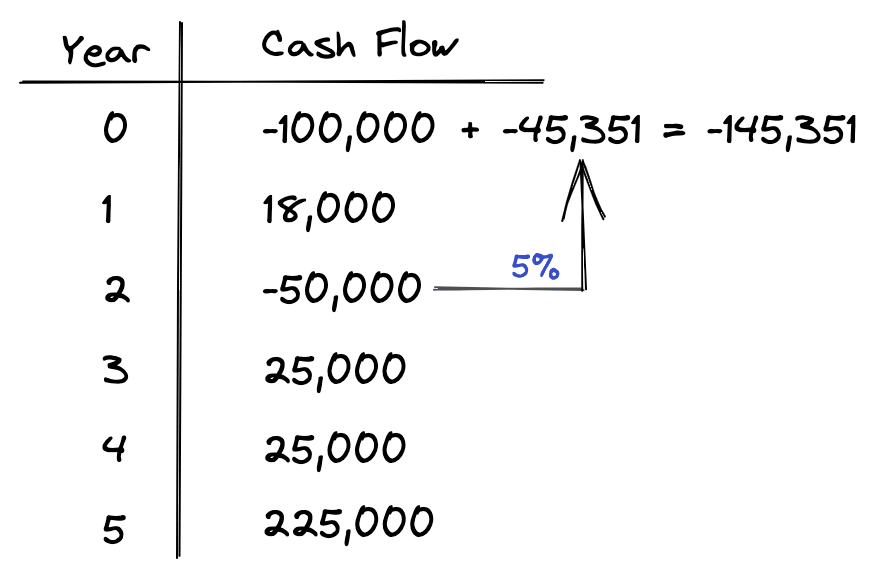
This simply tells us that if we want to have $50,000 available to spend in 2 years, then we need to set aside $45,351 today in an account earning 5% annually. So, now we’ve transformed our original set of cash flows into a new modified set of cash flows that has just two figures: a $145,351 initial investment and a $309,104 accumulated capital amount at the end of the holding period.
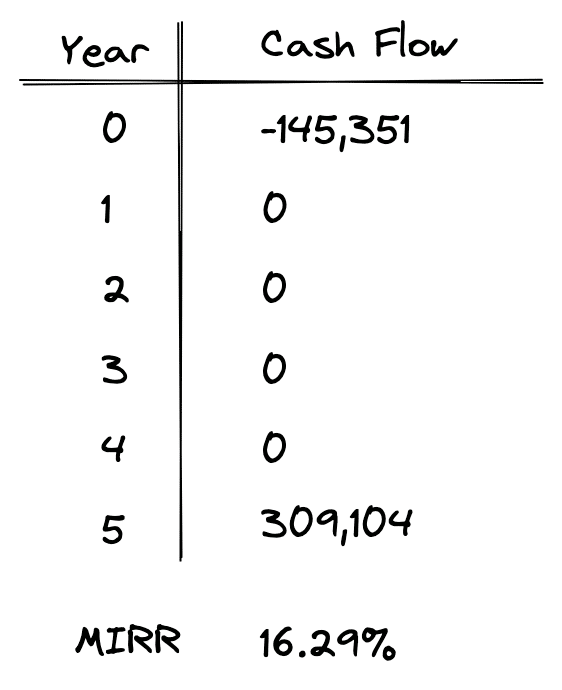
Now we can simply calculate an IRR on the above modified set of cash flows to get a Modified Internal Rate of Return of 16.29%. This modified internal rate of return now accounts for the funds we need to set aside today at a safe rate to fund future capital outlays. It also accounts for the reinvestment of all interim cash flows at our expected reinvestment rate.
How MIRR Solves the Multiple IRR Problem
You may recall that one of the problems with the traditional IRR calculation is that there are as many solutions to IRR as there are sign changes in a set of cash flows. Let’s take a look at an example set of cash flows:
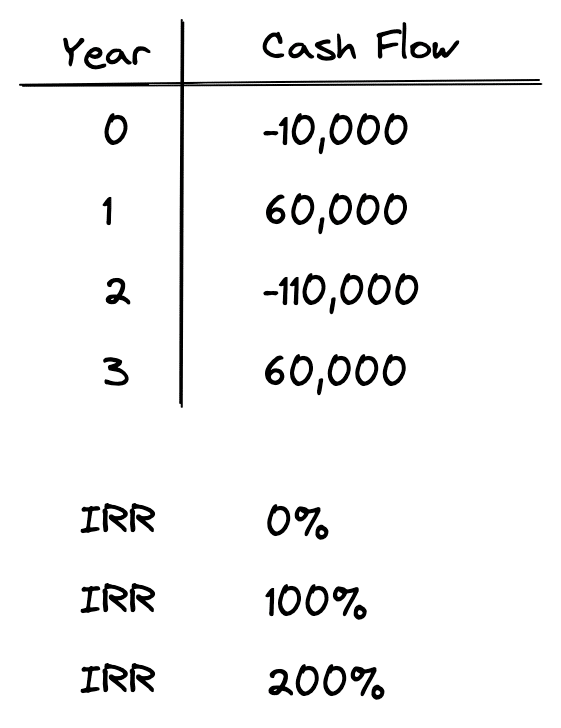
When you run an IRR calculation on the above set of cash flows, you indeed get multiple solutions. For the above set of cash flows we get 3 different IRR solutions: 0%, 100%, and 200%. So, which one is correct? The answer is that all of them are correct! Why is this? The short answer is that the IRR formula is not a linear equation, but instead it’s a polynomial which can generate multiple solutions. This is also the reason why the IRR function in Excel asks for a “guess” as an input. This is used to help Excel determine which solution is correct in case there are multiple solutions.
The good news is that the MIRR eliminates this well-known problem with IRR. To see how, let’s run the MIRR on the above set of cash flows using the same procedure we followed above. We’ll skip the interim steps of discounting negative cash flows at the safe rate and compounding interim positive cash flows at the reinvestment rate. However, this process is the same as we followed above, and it leaves us with the following modified set of cash flows:

And now when we calculate an IRR on this modified set of cash flows, we get 6.50%. Using the modified internal rate of return eliminates the multiple IRR problem because we are explicitly defining our safe rate and reinvestment rate. This boils the set of cash flows down to just two figures, resulting in a single MIRR figure.
MIRR Calculator
If you want to an easy way to calculate the modified internal rate of return, then check out our MIRR calculator. You can enter any number of cash flows, define a safe rate and a reinvestment rate, then you will instantly see your new set of cash flows along with your MIRR.
Conclusion
In this article, we discussed the logic and intuition behind the modified internal rate of return, or simply the MIRR. The MIRR is a powerful investment metric that is gaining in popularity since it eliminates the problems with the traditional IRR calculation and also provides a more realistic measure of return. In this article, we broke down the MIRR calculation step by step to make understanding the mechanics of MIRR easy to understand.
