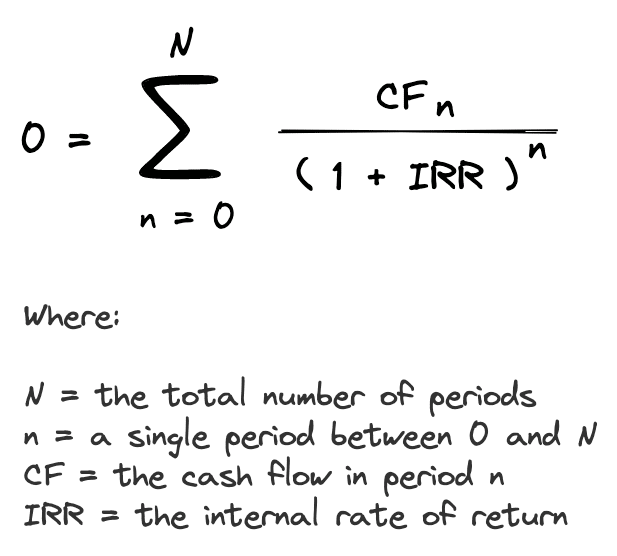XIRR: What You Should Know

The XIRR formula, included with Excel and other spreadsheet programs, is commonly used to measure investment performance in commercial real estate. The XIRR formula is popular because, unlike the IRR function, XIRR can handle irregular cash flow patterns. However, although XIRR is widely used, it is also widely misunderstood. In this article, we will take a deep dive into the XIRR formula and build an understanding of how it works from the ground up.

Here’s what we’ll cover:

• What is XIRR?
• XIRR Formula
• XIRR Example
• IRR vs XIRR
• What is an Effective Annual Rate?
• XIRR Day Count Conventions

What is XIRR?

XIRR is a Microsoft Excel function that stands for Extended Internal Rate of Return. The XIRR formula takes a set of cash flows and a set of dates for each cash flow, and then returns the effective annual rate that sets the net present value of those cash flows equal to zero. 

Contrary to a pervasive myth, XIRR does not use daily or continuous compounding. Instead, XIRR calculates an effective annual rate with annual compounding.

XIRR Formula

The XIRR function syntax in Excel has the following arguments:

XIRR(values, dates, [guess])

• Values (Required): A series of cash flows, with at least one positive and one negative. Payments are discounted using a 365-day year.
• Dates (Required): Payment dates matching the cash flows. Dates can be in any order but should be entered using the DATE function to avoid errors.
• Guess (Optional): Your estimate of the XIRR. If omitted, Excel assumes a default guess of 10%.

Here is the underlying equation used to calculate XIRR:

In the equation above, P_j is the j^th payment that is received d_j days after the starting date of the investment. The right side of the above equation discounts the cash flows to a present value. In other words, this solves for the effective annual rate that sets the net present value equal to zero. 

Excel uses an iterative method to calculate XIRR. Starting with the provided guess (or 10% if no guess is given), it repeatedly adjusts the rate until the result is accurate within 0.000001. If Excel can’t find a solution after 100 iterations, it returns a #NUM! Error.

XIRR Example

Let’s take a look at an example set of cash flows and calculate the XIRR. Suppose we have a $100,000 investment that generates monthly cash flows of $1,000 per month for 12 months, then we expect to sell the asset at the end of the year and net $100,000. What is the XIRR?

When we calculate the XIRR on this set of cash flows, we end up with 12.68%. The XIRR formula in Excel requires both a set of cash flows and a set of dates for each cash flow. In our example, this is what we plugged into the XIRR Excel formula:

Now that we know how to calculate the XIRR in Excel, let’s take a deeper dive into what the XIRR calculation actually means.

IRR vs XIRR

Recall that the Internal Rate of Return (IRR) finds the interest rate that sets the Net Present Value (NPV) equal to zero:

The key difference between IRR and XIRR is that while IRR finds the effective periodic rate that sets NPV equal to zero, XIRR finds the effective annual rate that sets the NPV equal to zero.

Differences in How IRR and XIRR are Calculated

IRR iteratively solves for the periodic interest rate that sets the net present value equal to zero:

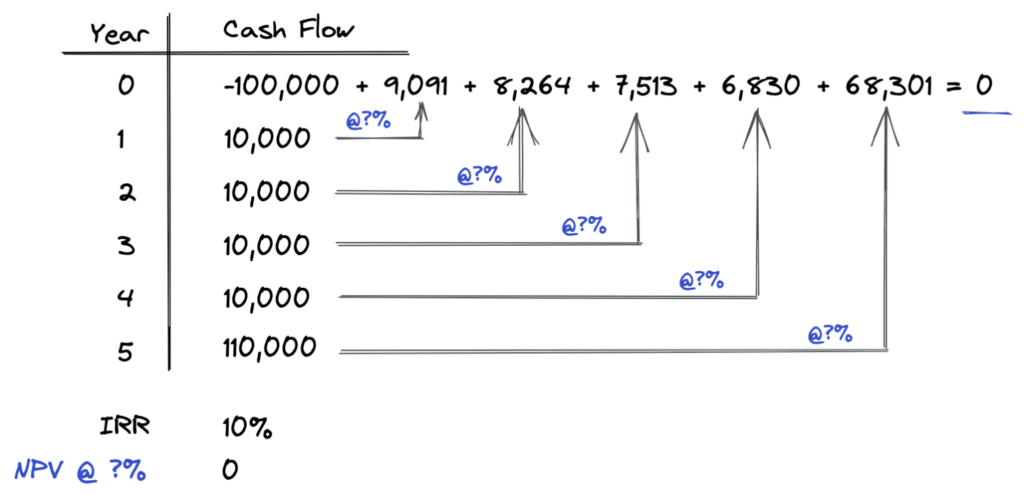
The IRR is the effective periodic rate that is the same for every period, since all periods must be equally spaced for IRR to calculate. IRR will always calculate an effective periodic rate based on the equal periodic spacing of your cash flows. For example, if you have monthly cash flows, IRR will calculate a monthly effective rate. If you have weekly cash flows, then IRR will calculate a weekly effective rate. 

On the other hand, XIRR iteratively solves for the effective annual rate that sets the net present value equal to zero:

Regardless of what the spacing of your cash flows is, XIRR will always return an effective annual rate. It does so, as illustrated, by using the actual number of days between cash flows and a 365-day year. By solving for the effective annual rate, and using the actual days between payments, XIRR can handle irregularly spaced cash flows.

XIRR Meaning

We can also see the difference between IRR and XIRR from another angle. 

A more intuitive way to define IRR is that it is the interest rate earned each period on the unrecovered investment balance. Consider the following set of cash flows:

At the start of month 1, the unrecovered investment balance is $100,000. Interest is due this month at a rate of 1% (the internal rate of return), which amounts to $1,000. With a total cash flow of $20,604, we pay off the interest and apply the remaining $19,604 toward reducing the investment balance. As a result, the balance at the beginning of month 2 is now $80,396, and this process continues until the entire unrecovered investment balance is paid off.

This is a more intuitive way to define IRR compared to the traditional textbook definition that IRR is the discount rate that causes the NPV to equal zero.

Likewise, XIRR can be thought of as the effective annual interest rate earned each period on the unrecovered investment balance, time-adjusted for the exact number of days in each period.

At the start of the first period, the unrecovered investment balance is $100,000. Over the first 31 days, interest is calculated based on a time-adjusted XIRR of 4.319%, which results in $4,319 of interest owed. The time-adjusted XIRR is calculated as (1+64.51%)^(31/365)-1.

A cash flow of $10,000 is received, which covers the interest and reduces the unrecovered balance by $5,681. This leaves an unrecovered balance of $94,319 at the beginning of the next period. 

At the start of the second period, the unrecovered investment balance is $94,319. Over the next 59 days, interest is calculated based on a time-adjusted XIRR of 8.379%, which results in $7,903 of interest owed. This time-adjusted XIRR is higher than the previous period due to the longer time frame (59 days vs 31 days). A cash flow of $10,000 is again received, which covers the interest of $7,903 and reduces the unrecovered balance by an additional $2,097. This leaves an unrecovered balance of $92,222 at the beginning of the third period.

The process repeats for each period, with interest calculated based on the time-adjusted XIRR for the number of days between cash flows. Each cash flow is applied first to the interest owed and then toward reducing the remaining balance, until the investment is fully recovered at the end.

What is an Effective Annual Rate?

Since XIRR solves for an effective annual rate, let’s take a short detour to review the math behind the effective annual rate. This will help you understand XIRR at a deeper level.

An effective interest rate considers the effects of compounding and gives the actual rate of increase over the stated time period. This contrasts with a nominal interest rate, which does not consider the effects of compounding over the stated time period.

In our article on effective vs. nominal rates, we explore these concepts and derive a formula widely used in finance for calculating the effective annual rate from the nominal interest rate and number of compounding periods.

For example, if we had a nominal annual interest rate of 6% compounded quarterly, then our effective annual rate would be 6.14%:

If we substitute the effective interest rate per compounding period i, where i = (r/m), then we can calculate the effective annual rate as follows:

For example, if we have an effective rate of 1% per month, we would convert this to an effective annual rate as follows:

Alternatively, if we know the effective annual rate and want to find the effective interest rate per compounding period, then we can also rearrange the equation above to solve for i:

For example, if we have an effective annual rate of 12.68% we could convert this to an effective monthly rate as follows:

Take note that these general effective rate formulas assume equally spaced compounding periods. However, this is not true for XIRR, which is a common source of confusion.

Let’s further explore this difference in the XIRR formula.

XIRR and The Effective Annual Rate

Let’s revisit the same XIRR example used earlier in this article. Suppose again that we have a $100,000 upfront investment that is expected to generate monthly cash flows of $1,000 per month for 12 months, then we expect to sell the asset at the end of the year and net $100,000. Earlier, we calculated an XIRR of 12.68%.

This time, let’s calculate the effective annual rate by hand using one of the general effective rate formulas instead of using Excel.

Since our cash flows are monthly, that means we can first solve for a monthly effective interest rate. We can do this by calculating IRR, or by using a financial calculator. Once we have a monthly effective rate, we can then convert this into an annual effective rate.

To find the monthly effective rate we can simply plug in -100,000 for PV, 12 for N, 1,000 for PMT, and 100,000 for FV. Then we can solve for i, which is 1.00%. Note that this is an effective monthly interest rate. You will get the same result if you calculate an IRR on these cash flows.

So, we have an effective monthly rate of 1%. Since we know the effective interest rate per compounding period, which is monthly, we can now plug this into the second equation from above to get:

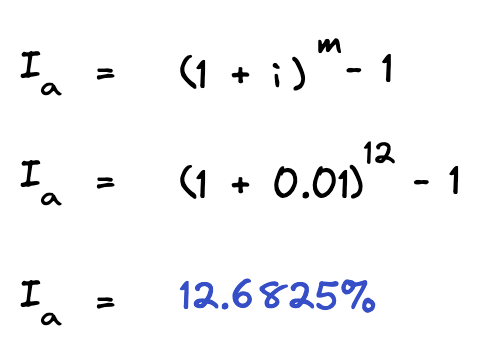
In other words, if we invest $100,000 upfront and get $1,000 per month for 12 months plus we get back our initial investment at the end of the year, then we will have earned a 12.68% effective annual rate of return. 

Notice that this is the same result we found by using the XIRR calculation in Excel. This is the same because the XIRR formula is also just solving for an effective annual rate.

But wait a minute!? I thought we said the XIRR calculation does not assume equally spaced compounding periods and therefore will produce a different result!

Indeed, some of you may have noticed that we do have a small problem.

If you expand our XIRR result and also our manually calculated effective annual rate out to 4 decimal places, you’ll see they are not exactly the same. 

The manually calculated effective annual rate is 12.6825%. But the XIRR we calculated was 12.6860%. If both procedures are calculating an effective annual rate, then why aren’t they exactly the same?

The short answer is that our manual calculation assumes 12 equally spaced compounding periods, while the XIRR uses the actual number of days in each compounding period and assumes a 365-day year.

Let’s take a deeper look at what this means.

XIRR and Day Count Conventions

The difference between the XIRR calculation and the manually calculated effective annual rate arises because XIRR uses an actual/365 day count convention, while the generalized formula does not.

Day count conventions are standardized methods used in finance to calculate interest accrual. They specify how days between periods are counted, defining month and year lengths for computing various time-based financial metrics.

Common day count conventions include:

1. Actual/365: Uses the actual number of days in each period and assumes 365 days per year.
2. Actual/360: Uses the actual number of days in each period but assumes 360 days per year.
3. Actual/Actual: Uses the actual number of days in each period and the actual number of days per year.
4. 30/360: Assumes 30 days per month and 360 days per year.

XIRR uses an actual/365 day count convention because the XIRR formula explicitly uses the actual number of days between each cash flow and a 365-day year. On the other hand, the generalized formula does not explicitly use any day count convention at all. This is why we end up with slightly different calculations.

Let’s take a look at some examples of when this matters.

XIRR Day Count Differences

To illustrate how this affects our calculations, let’s revisit our example using the XIRR formula with the actual day count. This time, we’ve changed the date to a leap year to add a twist.

• Initial investment: -$100,000 on January 1, 2024
• Monthly cash flows: $1,000 on the last day of each month
• Final cash flow: $100,000 on December 31, 2024

The XIRR formula is:

Notice that the dj in the exponent is the actual number of days, and in all cases XIRR uses a 365-day year. That means XIRR uses an actual/365 day count convention.

Let’s write out this equation for our example:

Note that 2024 is a leap year, so the last cash flow is on day 366.

Solving this equation (which is done by Excel iteratively) gives us r = 0.126476, or 12.66476%. This is how XIRR calculates the effective annual rate using the actual number of days between cash flows and a 365-day year. Also note that the rate is slightly lower than in non-leap years.

Now, let’s compare this to our manual calculation using the general EAR formula.

Using the same set of cash flows, we find the monthly effective rate is 1.00%. Again, to find the monthly effective rate we can solve for IRR, or use a financial calculator and plug in -100,000 for PV, 12 for N, 1,000 for PMT, and 100,000 for FV.

Now, we can use the following formula to convert this to an effective annual rate:

In this case, we have 12 equally spaced compounding periods per year:

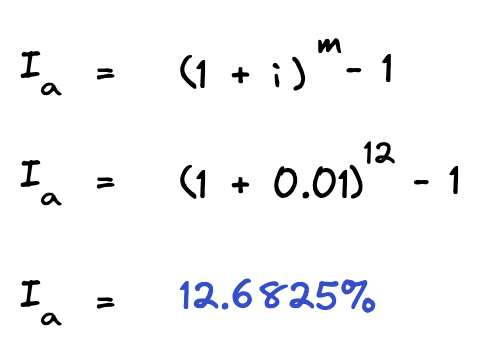
Although this general formula doesn’t explicitly define a day count convention, in this example it is consistent with a 30/360 convention because 30/360 reduces to 1/12 as a fraction. That is:

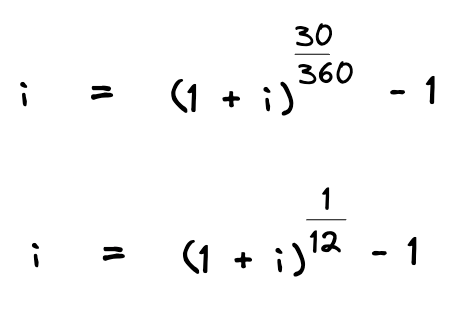
In other words, we use a 30/360 convention whenever we convert an effective annual rate to a monthly rate using (1+R)^1/12 -1, or whenever we convert a monthly rate to an annual effective rate using (1+R)^12 – 1.

So, in one method we solve directly for an effective annual rate using the actual number of days between cash flows, and a 365-day year. In the other method, we solve for a monthly effective rate, then convert this to an effective annual rate assuming there are 12 equally spaced months in a year.

Since we aren’t using the same method for both calculations, we end up with different results.

Differences when converting XIRR to a periodic rate

To see this in another way, let’s take our XIRR and go in the other direction by expressing it as a monthly effective rate. We can do this for the month of January, which has 31 days, as follows:

So when we directly solve for a monthly effective rate assuming 12 equal compounding periods, we get 1%. But if we start with XIRR and then convert it to a monthly rate, we end up with more than 1% for the month of January.

The reason this is more than 1% is that we are starting with XIRR, which calculates an effective annual rate using an actual/365 convention, then we are converting it to a monthly rate using a 31-day month. Instead of using 12 equal compounding periods, we are using the actual number of days between cash flows and a 365-day year.

What if we instead convert our XIRR to a monthly rate using the simplified formula that assumes 12 equally spaced periods? 

Now we get slightly less than 1%. Again, this doesn’t match the 1% monthly effective rate we solved for directly (using a financial calculator or IRR) because we are starting with XIRR, which calculates an effective annual rate using an actual/365 day convention. We then convert this to a monthly rate, assuming 12 equally spaced periods in the year, which is equivalent to a 30/360 day convention. Note that if you do these calculations directly on XIRR in Excel you will end up with slightly different results because of the extra precision used in Excel.

The key thing to remember is that the difference between these two results is due to the day count convention used in XIRR. When you are converting rates from yearly to monthly or monthly to yearly, be careful which method you use. This, of course, applies to other compounding periods as well, such as daily, weekly, quarterly, etc.

Although these differences might seem minor, they are a common source of confusion in waterfall modeling, and can lead to significant misunderstandings.

Using XIRR in Waterfall Calculations

To illustrate how these minor calculation differences can cause confusion in waterfall modeling, let’s look at an example. Let’s assume that an LP has a beginning capital balance of $5,000,000. The hurdle is a 20% effective annual rate. How much is the LP owed in the month of January to earn this hurdle?

You can probably see where this is going. The amount owed to the LP depends on how you convert the annual effective rate into a monthly effective rate.

You could use the XIRR method and calculate it as:

Alternatively, you could use the simplified approach to calculate the required return:

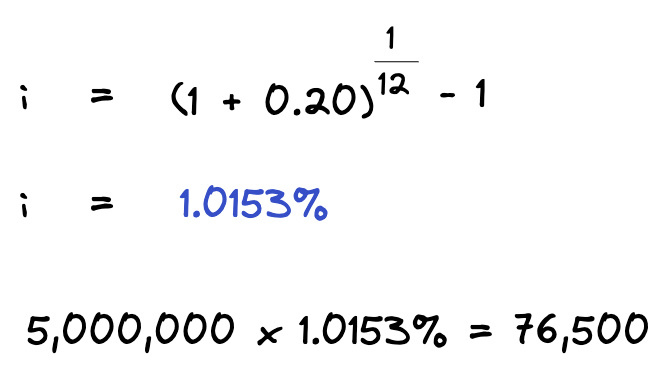
Although this difference may seem small —$78,000 versus $76,500 in just one month — these discrepancies in the returns owed to the LP can still cause misunderstanding, particularly over longer holding periods.

The same type of problem occurs when you calculate monthly distributions using one method, but then use a different method to error-check that your calculated monthly cash flows match your annual return hurdle.

For example, you might calculate your monthly distributions using the simplified method assuming 12 equal compounding periods, but then try to calculate an XIRR on your cash flows to verify they result in the correct hurdle rate. Since you use one method to convert the annual hurdle to the monthly distributions, but a different method to verify the monthly amounts equal the annual hurdle rate, this can lead to confusion over why an error-check exercise fails.

Misunderstanding around how these calculations are carried out can become sources of disagreement. While partnership agreements should clearly define these procedures, it’s unfortunately common for them to be vague and even contradictory on how the calculations are handled.

Conclusion

XIRR is a powerful tool in financial analysis, particularly for investment performance measurement in commercial real estate. Its ability to handle irregular cash flow patterns makes it more versatile than the standard IRR function. However, as we’ve explored, XIRR has some nuances that are important to understand:

1. XIRR vs. IRR: While IRR calculates an effective periodic rate, XIRR always returns an effective annual rate, regardless of the cash flow frequency.
2. Day Count Convention: XIRR uses an actual/365 day count convention, which means it considers the actual number of days between cash flows and assumes a 365-day year.
3. Calculation Differences: The XIRR result may differ slightly from manual calculations using generalized effective rate formulas due to differences in day count conventions.
4. Conversion Caution: When converting XIRR results to other periodic rates or vice versa, it’s important to be mindful of the underlying assumptions and day count conventions used.

Understanding these aspects of XIRR is essential for accurate financial modeling and analysis, particularly in contexts where precise timing of cash flows is important. While the differences in calculations may seem small, they can have significant implications in complex financial models or large-scale investments.