Modern portfolio theory is widely used in the world of finance. In this article we’ll take a closer look at what modern portfolio theory is, review an example calculation, and discuss the assumptions behind the theory.
What is Modern Portfolio Theory?
Modern portfolio theory (MPT) is widely used in finance and commercial real estate to create investment portfolios that maximize return for a given level of risk, or alternatively, minimize risk for a given level of return.
Harry Markowitz is known as the father of Modern Portfolio Theory (MPT). In 1952, While completing his doctoral dissertation in economics at the University of Chicago, Harry Markowitz published a portion of his research on “Portfolio Selection” in the Journal of Finance. This publication marked the beginning of a whole new vein of research into financial economics and investing. In 1990, Harry Markowitz received the Nobel Prize in Economics for his work on Modern Portfolio Theory. His work laid the foundation for how we think about investment decisions today.
Using MPT, investors not only considered the risk and return characteristics of individual assets but also the relationships among asset returns. The key to MPT is the idea of diversification benefits. In other words, investors should consider an optimal mix of differing assets to achieve the maximum return for the investor’s preferred level of risk.
Fundamentals of Modern Portfolio Theory
According to MPT, investors should not consider individual investments alone but as part of a portfolio of assets. This portfolio of assets should be constructed in a way that maximizes return for a given level of risk. Investors can also reduce their overall portfolio risk by diversifying their holdings through individual, unrelated assets. Thus, investors must consider the impact on the mean-variance characteristics of the portfolio when evaluating any new investment. Using MPT, the two most important characteristics of an asset are the expected return of the asset (mean) and the standard deviation of the returns (variance).
Modern Portfolio Theory Assumptions
Modern portfolio theory assumes investors are risk averse. This doesn’t mean that investors won’t take on risk, but prefer lower risk to higher risk. For example, if two investments yield 10% each but have standard deviation in those returns of 4% and 2%, the risk averse investor would prefer the asset with the 2% variation in return.
Risk averse investors also require a premium for taking on more risk. Therefore, assets with higher variance in their returns must compensate investors with higher expected returns. Risk averse investors will also prefer the asset with the highest expected return for a given level of risk. For example, if you have two assets with 4% standard deviation of returns but expected returns of 7% and 9%, the risk averse investor would choose the asset with 9% expected return.
Diversification allows an investor to reduce overall portfolio risk while achieving the investor’s required rate of return on the portfolio. Although diversification cannot reduce systematic risk (risk associated with the overall financial market), it can reduce what is known as idiosyncratic risk. An asset’s idiosyncratic risk is a measure of the variance in return attributed to that specific stock. This differs from the systematic risk associated with all investments in a market with uncertain outcomes. Diversification cannot reduce an investor’s exposure to systematic risk.
Ultimately, it is the correlation between asset return distributions that provide diversification benefits. If two assets have a correlation of 1.0, that means they have approximately the same return distribution. If one asset increases by 2%, the other should also increase by 2%. On the other hand, two assets with a correlation of -1.0 have just the opposite return distribution. If one asset increases by 2%, the other should decrease by 2%.
Modern Portfolio Theory and The Efficient Frontier
Graphing the standard deviation and expected return (risk and return) for all possible portfolios yields a picture like the one below.
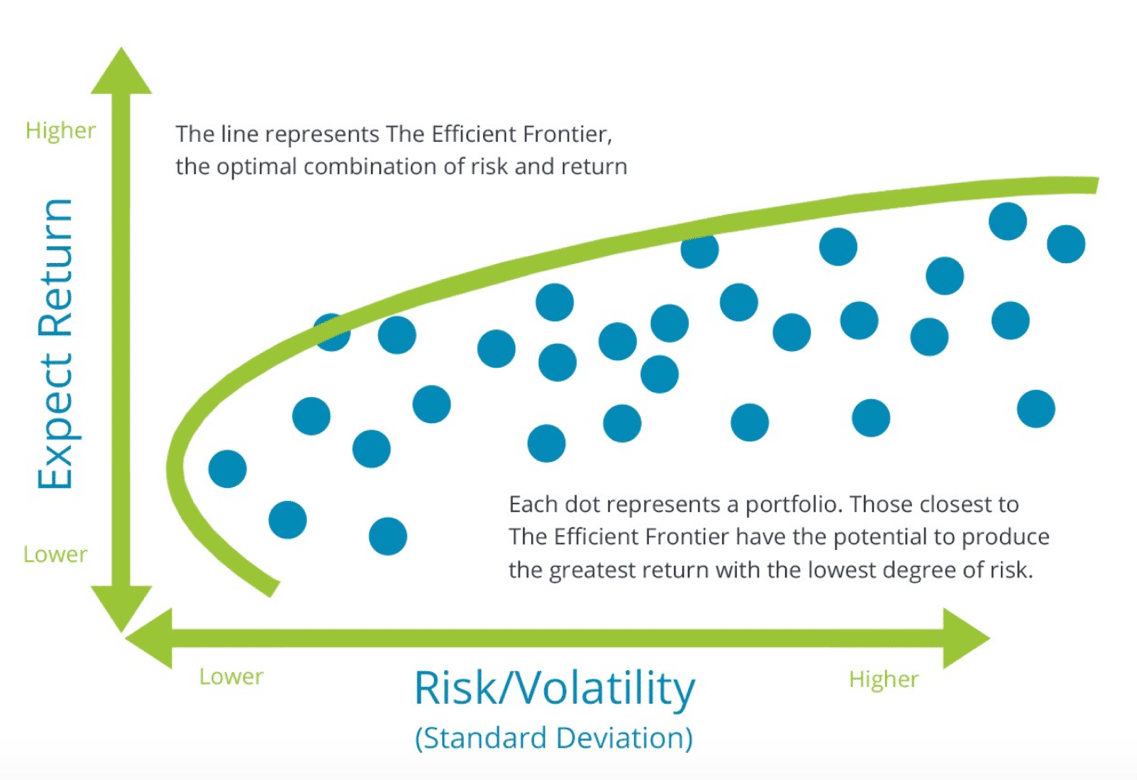
Since a rational, risk averse investor should always choose the portfolio with the highest expected return for a specific level of risk, the scatterplot of all portfolios illustrates a line that is known as the efficient frontier. Investments along the efficient frontier provide investors the highest expected return for a particular level of risk. All portfolios that are not located along the efficient frontier are suboptimal. The efficient frontier demonstrates the power of diversification because it contains a variety of portfolios that incorporate numerous investments in different ways.
Modern Portfolio Theory Example Calculations
To see how this works, start with two assets that will each have a weight of 50% in a portfolio. Property A has an expected return of 12% annually and 10% standard deviation of returns. Property B has an expected return of 9% annually and 8% standard deviation of returns. The risk-return tradeoff required by risk averse investors shows that higher expected returns are expected with higher risk of returns. The correlation of returns is 0.4.
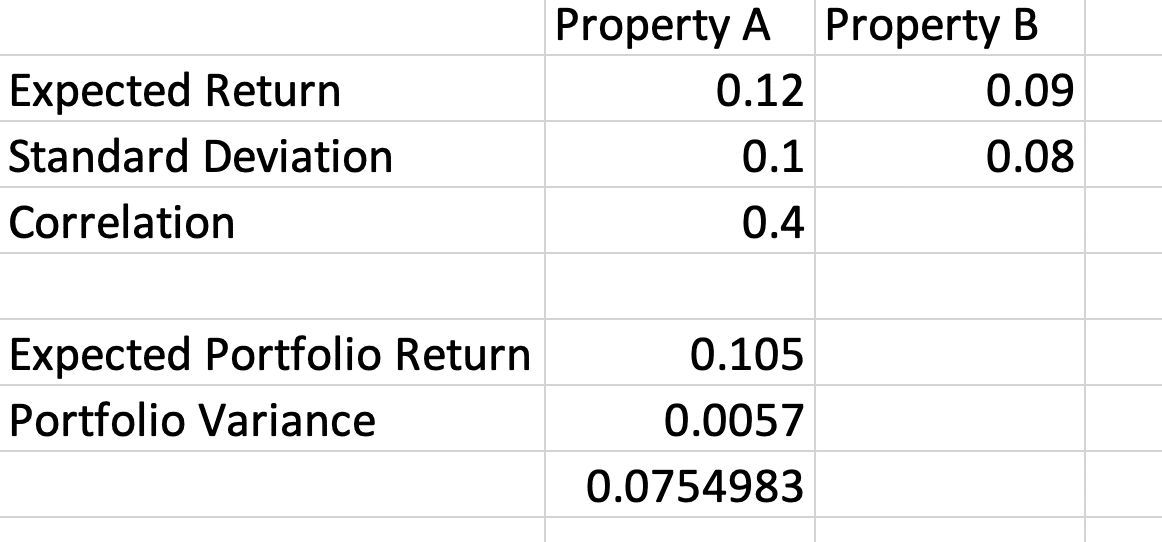
To calculate the expected return of the portfolio, find the weighted average of the returns of the two assets.
Expected Portfolio Return = (0.5)(.12) + (0.5)(.09) = .105 or 10.5% annually
The formula for portfolio variance is:
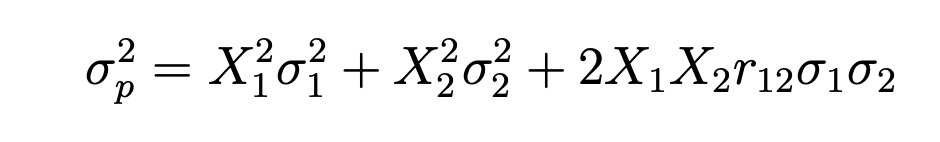
X1 = weight of asset 1
σ1 = standard deviation of asset 1
X2 = weight of asset 2
σ2 = standard deviation of asset 2
r12 = correlation coefficient of assets 1 and 2
So, in this example, the calculation for portfolio variance would be:
Portfolio Variance = (0.52)(0.12) + (0.52)(0.092) + (2)(0.5)(0.5)(0.4)(0.1)(0.09) = .0057
Taking the square root of the portfolio variance yields a portfolio standard deviation of .075 or 7.5% annually.
Therefore, this example shows the benefit of portfolio diversification according to modern portfolio theory. The portfolio of assets has a lower risk (standard deviation) than either of the two assets alone. The portfolio also earns a higher return for a lower level of risk than Property B in this example.
Post Modern Portfolio Theory
Software developers Brian Rom and Kathleen Ferguson introduced the concept of Post Modern Portfolio Theory (PMPT) in a 1993 publication in the Journal of Performance Management. PMPT is essentially an extension of Markowitz’s Modern Portfolio Theory because it keeps the risk and return tradeoff at its core. The definition of risk is the key difference between the two theories. Modern Portfolio Theory defines risk as the standard deviation of returns, and positive and negative returns are weighted equally. On the other hand, PMPT acknowledges that investors are far more concerned with the downside risk of an investment. In other words, investors care more about losing money than they do about making more money than they had expected. So, PMPT focuses entirely on the negative component of the return distribution in its risk calculation.
Conclusions
Modern Portfolio Theory still forms the basis for investment management and portfolio selection. Investors seek to maximize their return for a particular level of risk. They also use diversification across industries and asset classes to achieve the most efficient portfolio balance of risk and return. While new theories and models refine the behavioral tendencies with new technology, we have not moved too far away from Markowitz’s original theory.
