As sure as the sun rises, interest rates are going to go up and down over time. As they change, they have a profound effect on global financial markets, investors, banks, and corporate borrowers.
In the world of lending, both borrowers and debt issuers (lenders) have the ability to capitalize on interest rate movements by entering into derivative contracts called an Interest Rate Swaps. By doing so, either party can either: (1) obtain protection in a rising rate environment; or (2) obtain lower payments in a falling rate environment. However, both parties can’t be right. Interest Rate Swaps are a zero sum game, meaning one party is going to “win” and the other is going to “lose” depending on which way rates move.
Interest Rate Swaps are an advanced but important topic, and the purpose of this article is to provide an introduction to their utility in the world of real estate lending. To achieve that goal, I’m going to cover the following:
- What is an Interest Rate Swap?
- When is appropriate to use an Interest Rate Swap?
- What are the risks of entering into an Interest Rate Swap agreement?
- How are Interest Rate swaps priced?
- Interest Rate Swap example
What is an Interest Rate Swap?
An interest rate swap is a derivative contract whereby two parties (counterparties) agree to exchange one stream of interest payments for another, based on a specified rate index and principal amount.
In the world of real estate lending, the most common type of interest rate swap is a fixed for floating exchange. In this scenario, one party exchanges a fixed stream of interest rate payments for a floating rate stream of payments. The parties are called “counterparties” and the principal amount of the loan is referred to as the “notional” amount.
When is it Appropriate to use an Interest Rate Swap?
In the world of real estate, the motivation for entering into a swap typically falls into one of two categories:
- A borrower wants protection against their belief that interest rates will rise in the future. In this case they would exchange their variable rate payment for a fixed rate payment; or
- A borrower wants to capitalize on their belief that interest rates are going to fall in the future. In this scenario, they would exchange their fixed rate payment for a floating rate payment.
In either case, the transaction can only happen because one party believes rates are headed one way; while the other party believes rates are headed the other way. We’re working under the assumption that both parties are rational actors, but we also know that they both can’t be right. One of the counterparties is going to be right and the other is going to be wrong, which is why Interest Rate Swaps can be inherently risky. Depending on the notional (principal) amount involved, being on the wrong side of the swap can be a very costly proposition.
What are the Risks of Entering into a Swap Agreement?
Interest Rate Swap transactions contain risks for both parties involved and they fall into one of two categories:
- Interest Rate Risk: While each of the parties in the swap transaction may have a steadfast belief about where rates are headed, they don’t always move as expected. As such, Interest Rate Risk is the risk that rates don’t move as anticipated. Let’s use an example to drive that point home: Counterparty A is an owner/operator of a multi-family property with a $20MM, variable rate mortgage tied to the LIBOR index. They believe that interest rates are going to rise in the future so they enter into a swap contract with counterparty B. Under the terms of their contract, they exchange their variable rate payment for a fixed rate, protecting themselves from rising rates in the process. But, rates don’t rise, they fall. As a result, counterparty A ends up paying more than they need to (they “lose”) while counterparty B ends up paying less than they modeled (they “win”).
- Credit Risk: Implicit in the swap is the idea that both parties will be able to live up to their responsibilities as outlined in the terms of the agreement. The risk that one party or the other can’t perform as expected is Credit Risk. Revisiting the example above, it assumes that the Borrower will be able to continue to make their mortgage payments over the term of the swap agreement. If rates fall, counterparty B “wins”, but if rates fall and counterparty A stops making their payments, then counterparty B loses anyway.
Bottom line. Interest Rate Swaps can be risky and, before entering into an agreement, it is important to have a firm conviction on both the future direction of interest rates and the creditworthiness of the counterparty to perform as expected throughout the duration of the swap agreement.
How are Interest Rate Swaps Priced?
To determine the price, the first step is to identify the “legs” involved in the swap. In our example, there are 2: (1) the fixed rate leg; and (2) the floating rate leg. Graphically, it can be depicted like this:
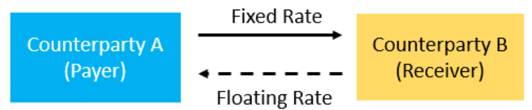
In our example Counterparty A will pay a fixed rate to Counterparty B. In return, Counterparty B will pay a floating rate to Counterparty A.
Now, to determine the price, we need to determine the present value of the cash flows for each leg. For the fixed leg, the equation is:
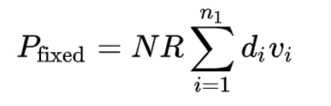
Pfixed: The present value of cash flows at the fixed rate
N: Notional Amount
R: Fixed Rate
n1: The number of payments
di : The day count fraction of the accrual in the i’th period, in decimal form
vi : The discount factor associated with the payment date in the i’th period
The floating rate leg has a similar equation:
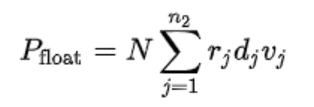
Pfloat : The present value of cash flows for the floating rate leg
N: Notional Amount
N2: Number of payments in the floating rate leg
Rj: The forecast rates of the index on which the price is based (LIBOR)
Dj: The day count fraction of the accrual in the j’th period, in decimal form
Vj: The discount factor associated with the payment date in the j’th period
Once the legs are calculated, the last step is to subtract them to get the price of the swap:
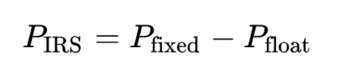
The price of the interest rate swap is equal to the present value of the fixed leg minus the present value of the floating leg.
Interest Rate Swap Example
To bring it all together, let’s go through an example of how a swap may be priced. It can get really complicated so we’re just going to go through a basic vanilla example. Here’s the scenario:
Counterparty A and Counterparty B enter into a swap agreement with a notional amount of $1 million. Counterparty A thinks that interest rates are going to rise and wants to potentially profit from them. Counterparty B is currently receiving a floating rate, but thinks rates are going down and wants to have it fixed.
Counterparty A offers Counterparty B a fixed rate of 7% in return for receiving a floating rate of LIBOR plus 2%. At the time of the agreement, LIBOR is 5%, valuing both legs of the swap at the same amount (Counterparty A has a fixed rate of 7%, Counterparty B has LIBOR + 2% = 7%). The agreement has a term of two years with quarterly payments.
Fast forward 3 months and LIBOR has risen to 6%, making the LIBOR + 2% calculation equal to 8%. As such, the first payments will be calculated as:
Counterparty A (Pays fixed rate, receives floating rate): $1,000,000 * .07% = $70,000
Counterparty B (Pays floating rate, receives fixed rate): $1,000,000 * .08 = $80,000
To eliminate the hassle of exchanging full payments, the parties would only pay the difference. As such, Counterparty B would pay $10,000 to Counterparty A. In this scenario, Counterparty B has incurred a $10,000 “loss”, meaning that they ended up paying $10,000 more than they would have if they had stuck with a fixed rate.
To value all streams of the swap agreement, cash flows are discounted to the present value.
Conclusion
While not for everyone, Interest Rate Swaps are a useful instrument that can protect against interest rate movements or allow an investor to profit from them. In either case, the swap participants need to have a firm conviction on where rates are headed before entering into the contract. One of them will be right and “win” while the other will be wrong and “lose.’
