How Not to Use NPV in Excel

NPV in Excel is widely used but commonly misunderstood. Even top MBA grads commonly misuse NPV in Excel. In this short article, we’ll look at the problem with NPV in Excel, show you where most people go wrong, and we’ll also walk through the correct way to use the NPV function in Excel, step-by-step.

The Problem With NPV in Excel

First, what’s the problem with NPV in Excel? Why do so many people get it wrong? Well, contrary to popular belief, NPV in Excel does not actually calculate the Net Present Value (NPV). Instead, it calculates the present value of a series of cash flows, even or uneven, but it does NOT net out the original cash outflow at time period zero. This original cash outflow actually needs to be manually subtracted out when using the NPV formula in Excel.

Before we jump into an example, let’s first take a step back to get some context and understand what NPV actually means in finance. NPV is simply the difference between value and cost. In other words, to find NPV we just take the present value of a series of future cash flows at a particular discount rate, then simply subtract out what our original cost is to acquire that stream of cash flows. Check out the Intuition Behind IRR and NPV for more on how this works.

Unfortunately, Excel does not define the NPV function in this way where it automatically nets out the original investment amount. This is where most people get stuck. Instead, NPV in Excel is just a present value function that gives you the present value of a series of cash flows. Then, it’s up to you to net out the original investment amount in order to find the actual NPV.

How Not to Use NPV in Excel

Let’s take an example. Suppose we have the following series of cash flows:

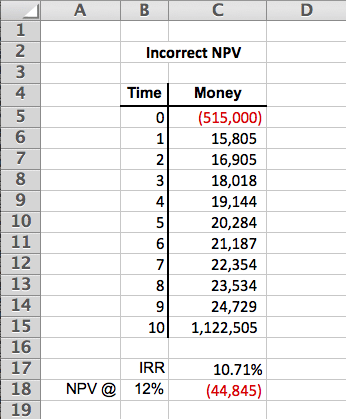
The above NPV calculation of -$44,845 incorrectly includes the $515,000 initial cash outlay in the series of cash flows. Here’s the exact formula used in cell C18 to incorrectly calculate NPV:

=NPV(B18,C5:C15)

Rather than calculating the correct NPV at time period 0, which is what we are interested in, what the above formula actually does is calculate the NPV at time period -1. Sure, you can manually adjust this forwards in time 1 period by multiplying by (1+r), substituting in our discount rate for r (12% in this case). This will adjust the formula above to give you the correct result, but it’s pretty confusing to most people and there is an easier way to do this.

How to Correctly Calculate NPV in Excel

The easier way to correctly calculate NPV in Excel is to exclude the initial cash outflow from your NPV formula. This will give you the present value of only the future cash flows. Then, you can simply net our your initial cash outlay from this present value of future cash flows calculation. Because the net present value is simply value minus cost, this approach is much more intuitive to most people.

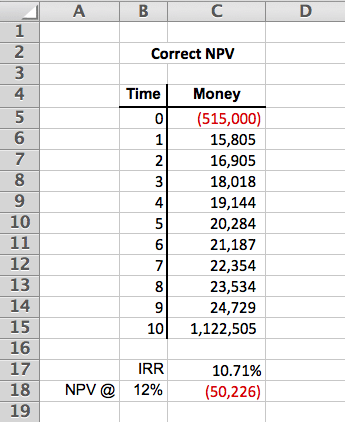
The above NPV calculation of -$50,226 correctly excludes the $515,000 initial cash outlay in the series of cash flows and then nets it out from the result of the NPV formula in Excel. Here’s the exact formula used in cell C18 to correctly calculate NPV above:

=NPV(B18,C6:C15)+C5

This correctly calculates the present value of our future cash flows (time periods 1 thru 10), which we can then take and net against our initial cash outlay of $515,000 (time period 0) in order to find the correct NPV.

Conclusion

NPV in Excel is widely used but commonly misunderstood. In this post, we discussed the problem with NPV in Excel, talked about why it’s so commonly misused, and then we walked through an example to illustrate the right and wrong way to use NPV in Excel. Keep this in your toolkit whenever you find yourself working with NPV in Excel, and avoid any unnecessary mistakes.